Algorithms Roadmap
Day 3: Valid Parentheses
Problem Statement
Valid Parentheses: Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string has valid parentheses.
Approaches:
Lets consider the following two approaches for this problem, and they both follow a similar strategy. The idea is to iteratively remove the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) until either the input becomes empty or we encounter an invalid structure.
Approach 1: Replace sub-strings
Continuously replace the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) with empty sub-string. If no such occurrence can be found and the input string is not empty, it indicates the input string is not a valid parentheses.
Complexity: Time complexity of the replaceAll operation is typically O(n*m), where n is the length of original string and m is the length of the substring that we are replacing with. However, in this case we are replacing with an empty string so the replaceAll time-complexity will be O(n). In the worse case, this operation needs to be performed n/2 times, so this overall time-complexity is O(n^2).
Approach 2: Stack approach
In this approach, a stack data structure is used to store the input string characters sequentially. As we traverse the input string from left to right, we continuously remove valid parentheses from the stack. When we encounter a closing bracket, we verify whether the top of the stack contains the corresponding opening bracket. If not, the input string is invalid parentheses.
Complexity: Since we process each character of the input string one-by-one, adding and removing elements from the stack is constant time. Therefore, the overall time complexity for this approach is O(n). The linear time complexity of this approach makes it a better approach than replacing sub-strings.
Code Implementation
Approach 1
class Solution {
public boolean isValid(String s) {
while(s.length()>0) {
String s2;
s2 = s.replaceAll("\\(\\)", "");
s2 = s2.replaceAll("\\[\\]", "");
s2 = s2.replaceAll("\\{\\}", "");
if(s2.length() != s.length()){
s = s2;
continue;
}
return false;
}
return true;
}
}
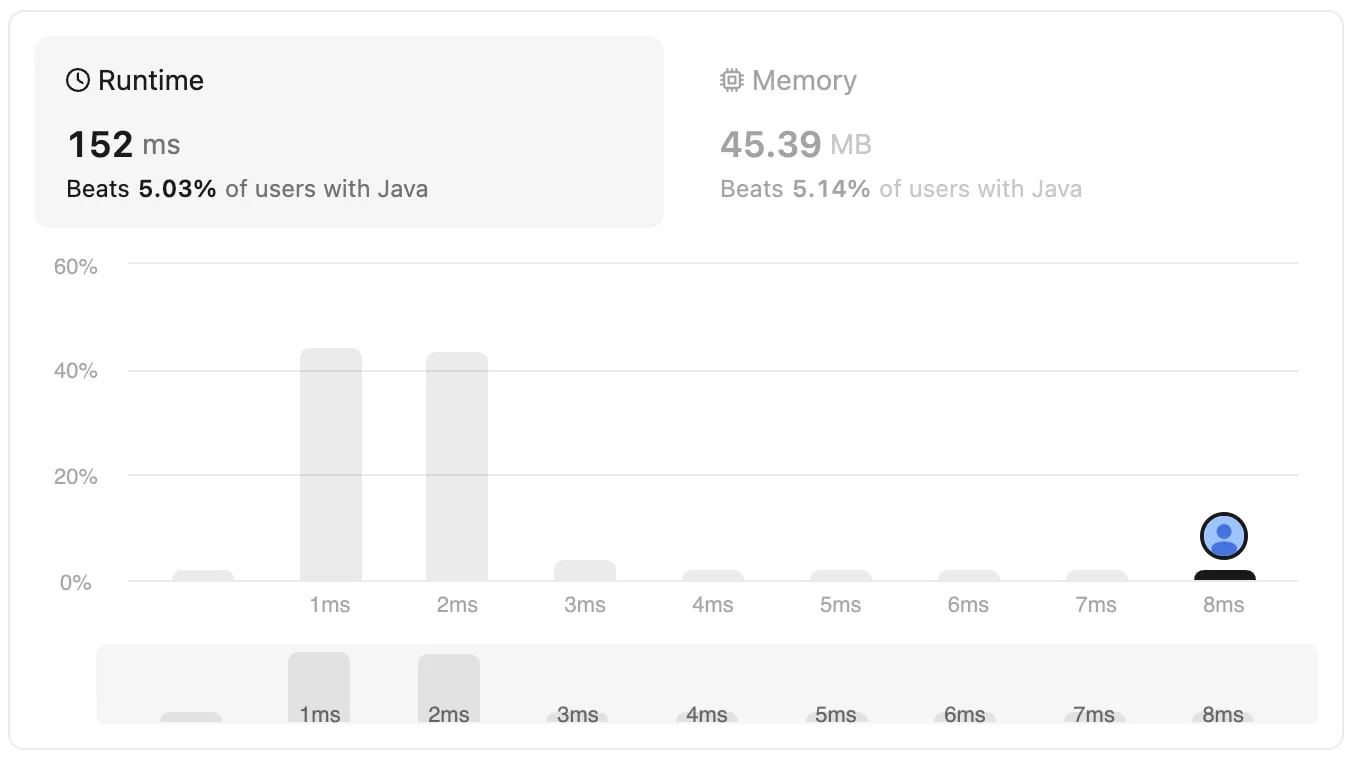
Approach 2
class Solution {
public boolean isValid(String s) {
Stack stack = new Stack<>();
for(char c: s.toCharArray()) {
if(c == '(' || c == '[' || c == '{') {
stack.push(c);
continue;
}
if(stack.isEmpty()) return false;
if(c == ')' && stack.peek() != '(') return false;
if(c == ']' && stack.peek() != '[') return false;
if(c == '}' && stack.peek() != '{') return false;
stack.pop();
}
return stack.isEmpty();
}
}
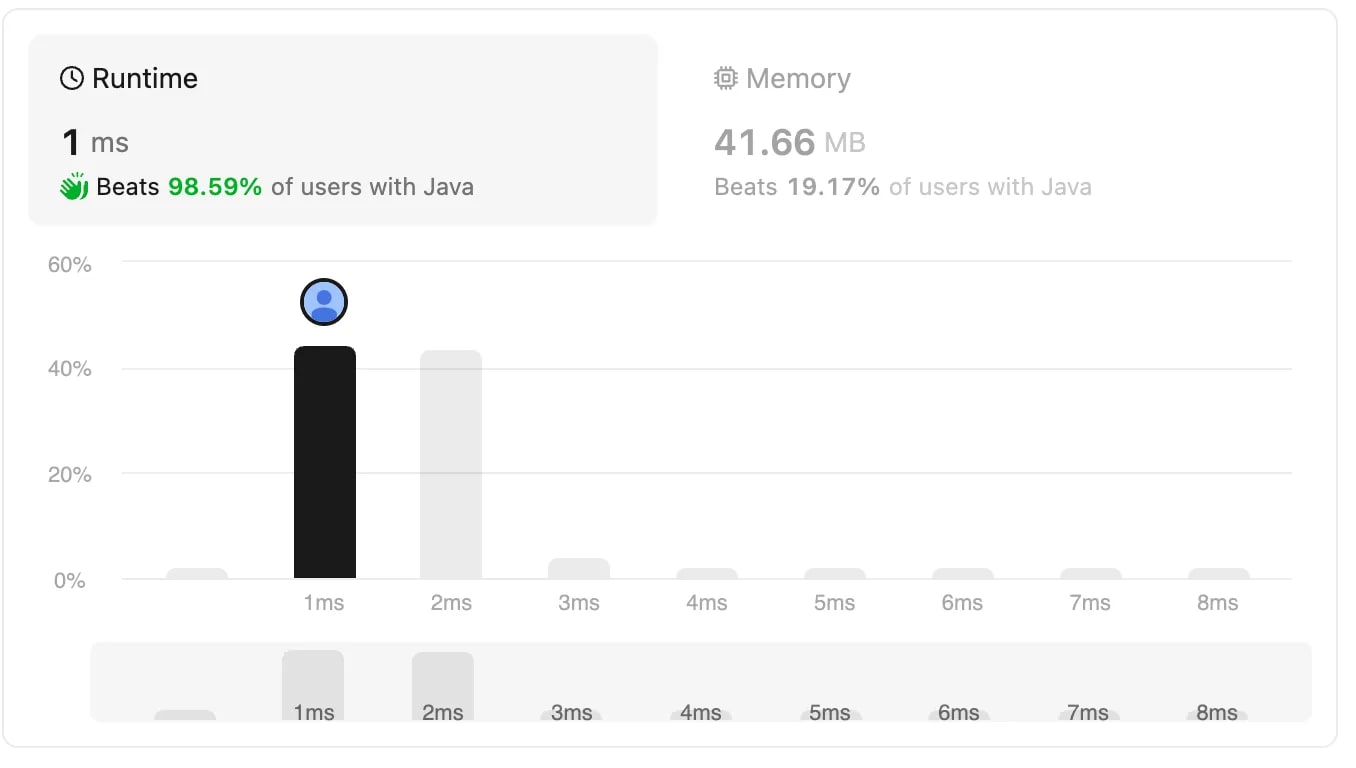
Final Thoughts
In conclusion, the runtime analysis of the approaches discussed clearly shows the importance of prioritizing O(n) solutions over O(n^2) solutions.
Day 3 - Valid Parentheses
Problem Statement
Valid Parentheses: Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string has valid parentheses.
Approaches:
Lets consider the following two approaches for this problem, and they both follow a similar strategy. The idea is to iteratively remove the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) until either the input becomes empty or we encounter an invalid structure.
Approach 1: Replace sub-strings
Continuously replace the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) with empty sub-string. If no such occurrence can be found and the input string is not empty, it indicates the input string is not a valid parentheses.
Complexity: Time complexity of the replaceAll operation is typically O(n*m), where n is the length of original string and m is the length of the substring that we are replacing with. However, in this case we are replacing with an empty string so the replaceAll time-complexity will be O(n). In the worse case, this operation needs to be performed n/2 times, so this overall time-complexity is O(n^2).
Approach 2: Stack approach
In this approach, a stack data structure is used to store the input string characters sequentially. As we traverse the input string from left to right, we continuously remove valid parentheses from the stack. When we encounter a closing bracket, we verify whether the top of the stack contains the corresponding opening bracket. If not, the input string is invalid parentheses.
Complexity: Since we process each character of the input string one-by-one, adding and removing elements from the stack is constant time. Therefore, the overall time complexity for this approach is O(n). The linear time complexity of this approach makes it a better approach than replacing sub-strings.
Code Implementation
Approach 1
class Solution {
public boolean isValid(String s) {
while(s.length()>0) {
String s2;
s2 = s.replaceAll("\\(\\)", "");
s2 = s2.replaceAll("\\[\\]", "");
s2 = s2.replaceAll("\\{\\}", "");
if(s2.length() != s.length()){
s = s2;
continue;
}
return false;
}
return true;
}
}

Approach 2
class Solution {
public boolean isValid(String s) {
Stack stack = new Stack<>();
for(char c: s.toCharArray()) {
if(c == '(' || c == '[' || c == '{') {
stack.push(c);
continue;
}
if(stack.isEmpty()) return false;
if(c == ')' && stack.peek() != '(') return false;
if(c == ']' && stack.peek() != '[') return false;
if(c == '}' && stack.peek() != '{') return false;
stack.pop();
}
return stack.isEmpty();
}
}

Final Thoughts
In conclusion, the runtime analysis of the approaches discussed clearly shows the importance of prioritizing O(n) solutions over O(n^2) solutions.
Sponsor Us|Community|Blog|Youtube
Have Feedback or want to contribute? Email: hello[@]100DaysOfCode.io
100DaysOfCode@2024