100 Days of Algorithms challenges

Problem Statement:

Valid Anagram - Given two strings `s` and `t`, return `true` if `t` is an anagram of `s`, and `false` otherwise.

Lets consider the following two approaches for this problem:

Approach 1: Sorting input strings

Anagrams return identical strings when sorted, so the simplest approach is to sort the input strings and compare. The input string can be sorted by splitting it into character array, performing the sort operation on the character array, and then join the sorted characters into a string.

Complexity: This approach uses extra O(n) space ( n = length of string) for character array and sorting the array makes it O(nlogn) time complexity.

Approach 2: Character frequency comparison

Second approach involves computing the frequency of each character in both strings. If any character’s frequency differs between the two strings, they are not anagrams. HashMap can be used to store the character frequencies since the updates can be done in constant time.

Complexity: This approach uses extra O(n) space for storing character HashMap. The time complexity is O(n) since we’ll be updating the HashMap for every character of the input strings.

Code Implementation:

Approach 1

  
    class Solution {
        private String sortedString(String s) {
            char c[] = s.toCharArray();
            Arrays.sort(c);
            return  Arrays.toString(c);
        }
        public boolean isAnagram(String s, String t) {
            return sortedString(s).equals(sortedString(t));
        }
    }
   

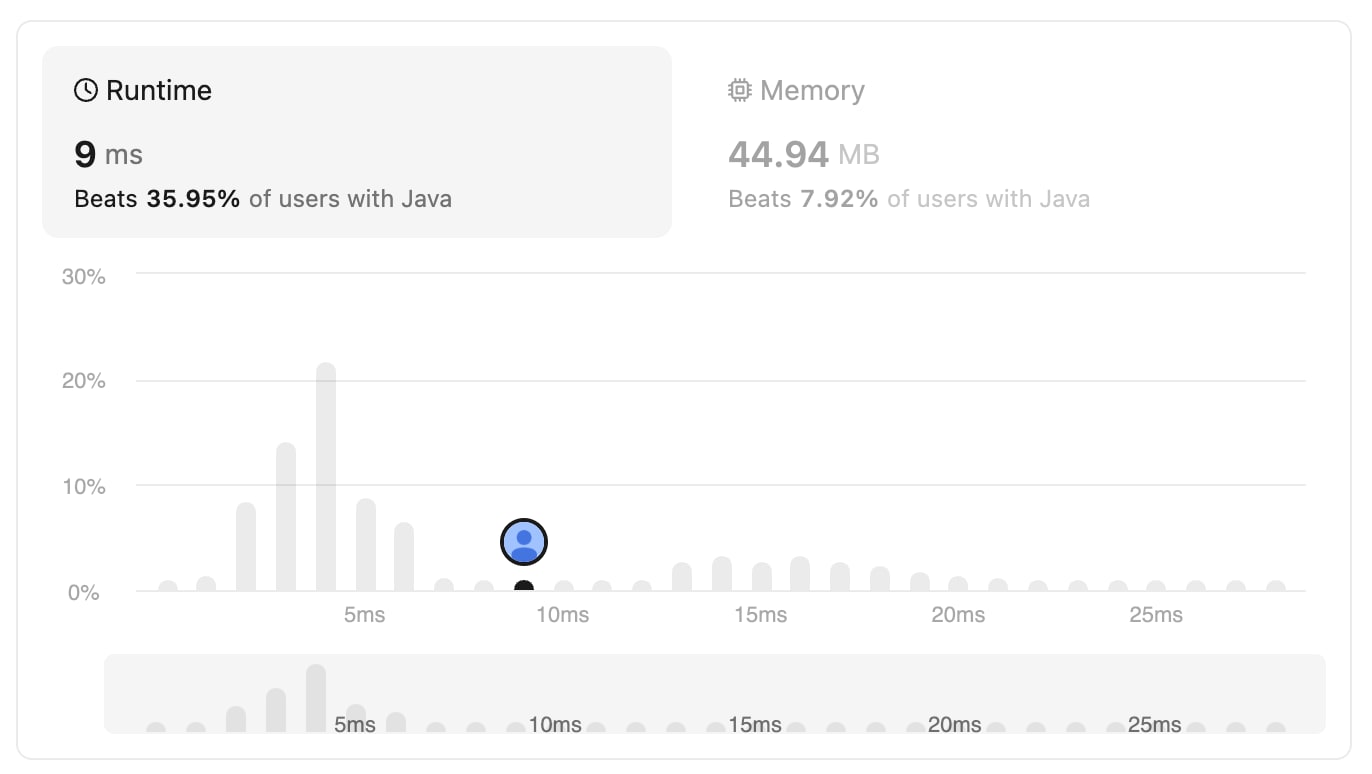
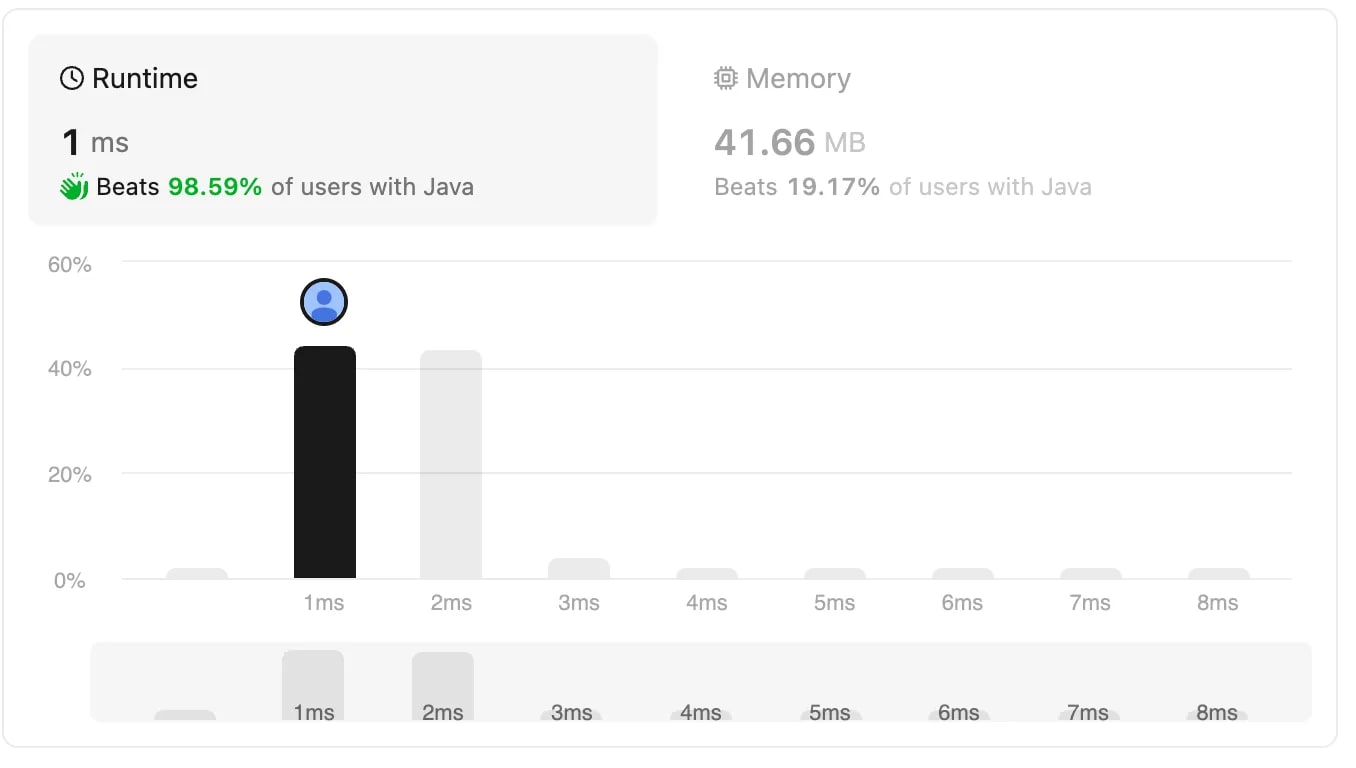
This implementation beats 35% users runtime which is acceptable. Arrays.toString(c) constructs the string via StringBuilder, it appends each character one by one, resulting in O(n) time complexity. Let’s explore if there would be any improvement by replacing it with String.valueOf(c) which takes constant time complexity.

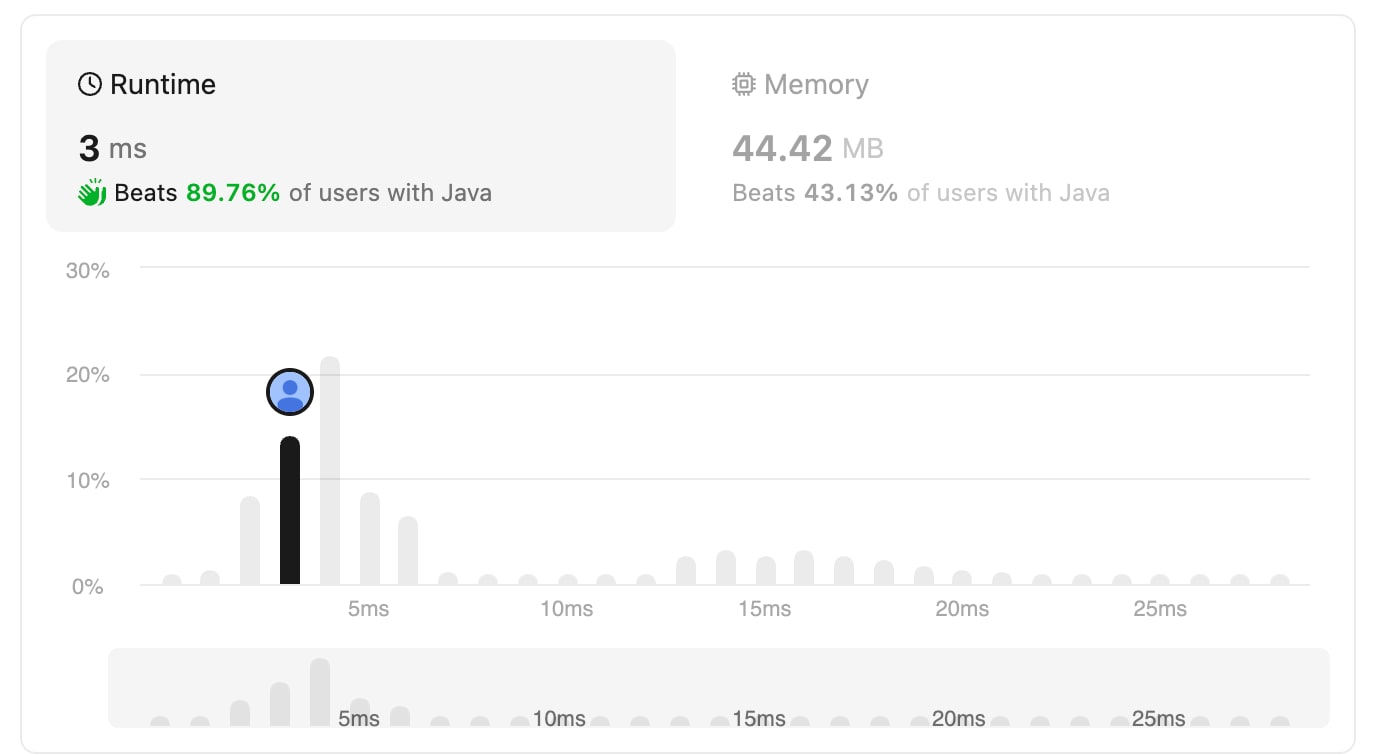
A single line change improved the runtime from 35% to 89%. Although, its only a minor improvement in memory but it beat 43% users compared to the previous 8%.

Approach 2

  
    class Solution {
        public boolean isAnagram(String s, String t) {
            if (s.length() != t.length()) {
                return false;
            }
            HashMap hm = new HashMap<>();
            for (char c : s.toCharArray()) {
                hm.put(c, hm.getOrDefault(c, 0) + 1);
            }
            for (char c : t.toCharArray()) {
                if(!hm.containsKey(c) || hm.get(c)==0) return false;
                hm.put(c, hm.get(c) - 1);
            }
            return true;
        }
    }
   

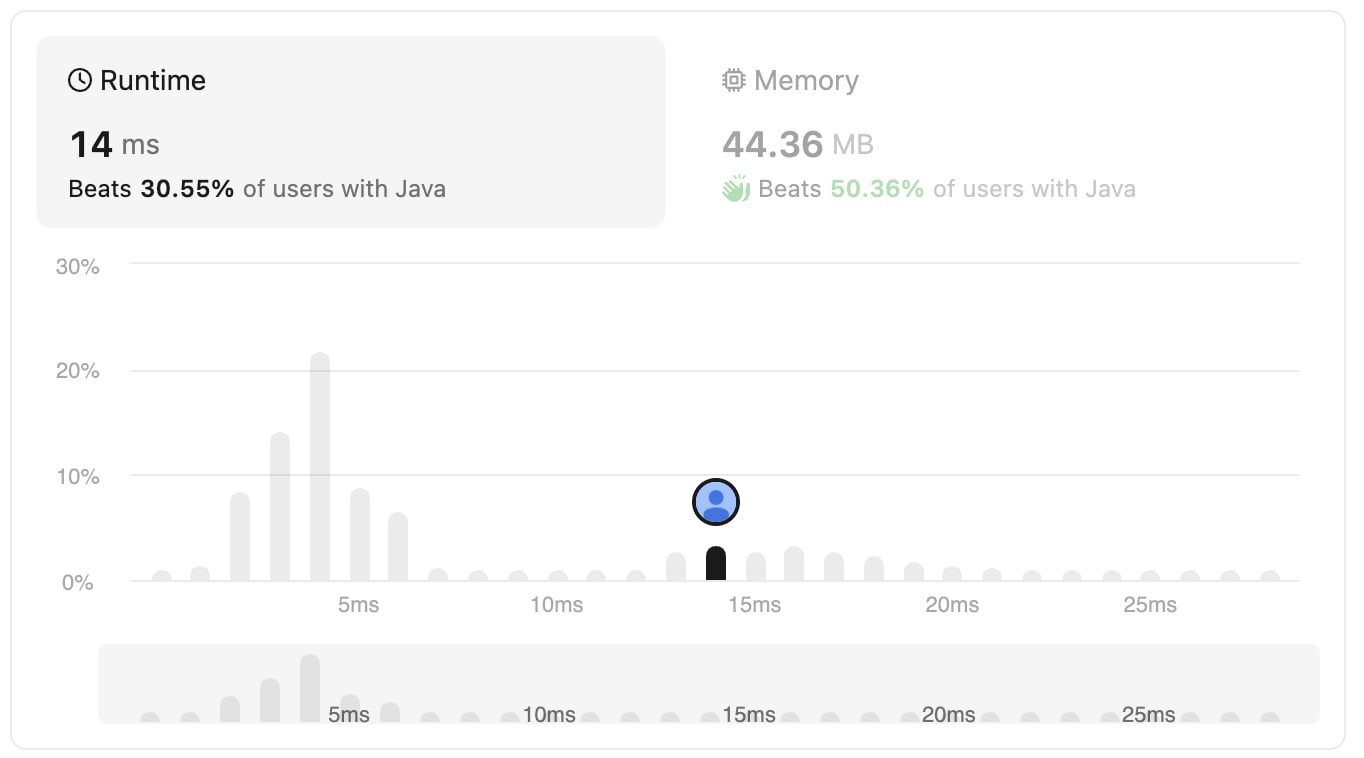
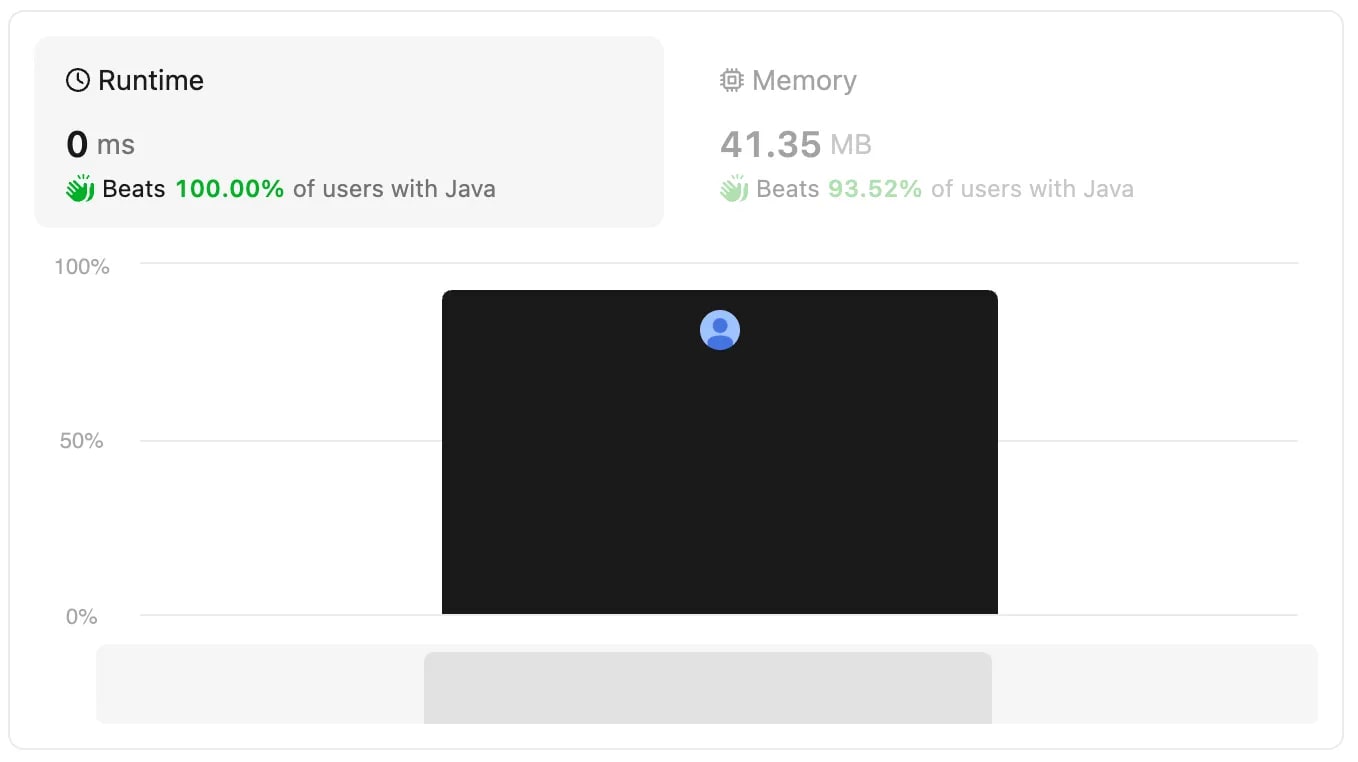
It's surprising to find that the approach 2 performed worse than approach 1. One possible explanation could be that there’s a constraint on the input string size, making log(n) effectively a constant. Going for a more complex approach by storing the frequencies of characters, didn’t provide any advantage.

Final thoughts

In an actual interview scenario, I would certainly choose the second approach, even if it appears to have lower performance in this specific case. Although this is a straight forward question, solving it sparked my curiosity.

We often prefer solutions with O(n) time complexity over those with O(nlogn), but does this translate to better performance in real-world scenarios?

Problem Statement

Valid Parentheses: Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string has valid parentheses.

Approaches:

Lets consider the following two approaches for this problem, and they both follow a similar strategy. The idea is to iteratively remove the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) until either the input becomes empty or we encounter an invalid structure.

Approach 1: Replace sub-strings

Continuously replace the smallest valid parentheses (i.e ‘()’, ‘[]’, ‘{}’) with empty sub-string. If no such occurrence can be found and the input string is not empty, it indicates the input string is not a valid parentheses.

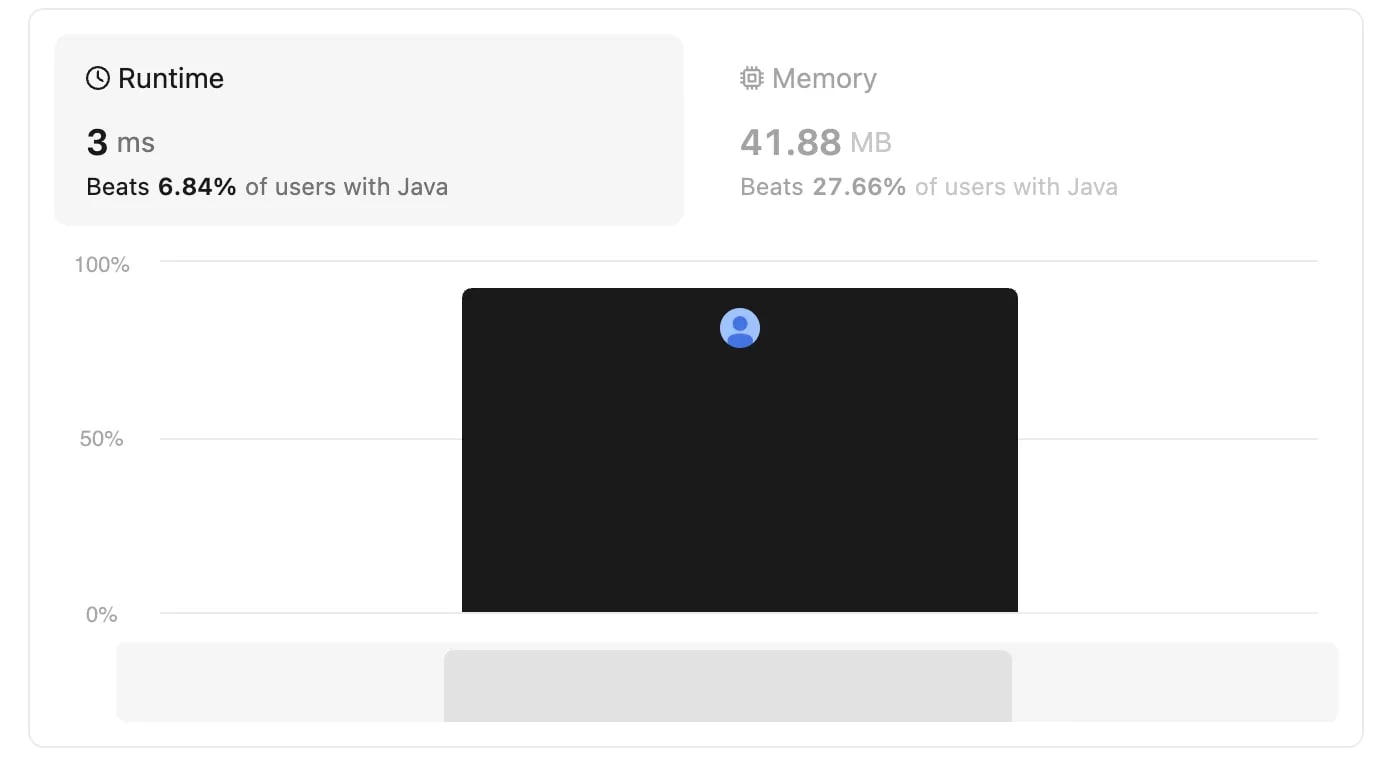
Complexity: Time complexity of the replaceAll operation is typically O(n*m), where n is the length of original string and m is the length of the substring that we are replacing with. However, in this case we are replacing with an empty string so the replaceAll time-complexity will be O(n). In the worse case, this operation needs to be performed n/2 times, so this overall time-complexity is O(n^2).

Approach 2: Stack approach

In this approach, a stack data structure is used to store the input string characters sequentially. As we traverse the input string from left to right, we continuously remove valid parentheses from the stack. When we encounter a closing bracket, we verify whether the top of the stack contains the corresponding opening bracket. If not, the input string is invalid parentheses.

Complexity: Since we process each character of the input string one-by-one, adding and removing elements from the stack is constant time. Therefore, the overall time complexity for this approach is O(n). The linear time complexity of this approach makes it a better approach than replacing sub-strings.

Code Implementation

Approach 1

  
        class Solution {
            public boolean isValid(String s) {
                while(s.length()>0) {
                    String s2;
                    s2 = s.replaceAll("\\(\\)", "");
                    s2 = s2.replaceAll("\\[\\]", "");
                    s2 = s2.replaceAll("\\{\\}", "");
                    if(s2.length() != s.length()){
                        s = s2;
                        continue;
                    }
                    return false;
                }
                return true;
            }
        }
   

Approach 2

  
        class Solution {
            public boolean isValid(String s) {
                Stack stack = new Stack<>();
                for(char c: s.toCharArray()) {
                    if(c == '(' || c == '[' || c == '{') {
                        stack.push(c);
                        continue;
                    }
                    
                    if(stack.isEmpty()) return false;
                    if(c == ')' && stack.peek() != '(') return false;
                    if(c == ']' && stack.peek() != '[') return false;
                    if(c == '}' && stack.peek() != '{') return false;
                    stack.pop();
                }
                return stack.isEmpty();
            }
        }
   

Final Thoughts

In conclusion, the runtime analysis of the approaches discussed clearly shows the importance of prioritizing O(n) solutions over O(n^2) solutions.

Problem Statement

Plus One - You are given a large integer represented as an integer array `digits`, where each `digits[i]` is the `ith` digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading `0`'s.

Increment the large integer by one and return the resulting array of digits.

Approach

This question brought back memories of how I used to do additions when I was a kid. It’s a fairly straightforward problem, we can perform an in-place addition by adding 1 to the last index. If the result is more than 10, we maintain a carry and add it to the previous cell. This process is continued till the carry is 0.

One edge case to consider is when the input consists of all nines. In this scenario, the array size will increase by one, so in-place modification won’t work. We’ll need to initialise a new array to accommodate the new digit. Either, check for this case in the beginning or at the end.

Code Implementation

  
        class Solution {
            public int[] plusOne(int[] digits) {
                int carry = 1;
                for(int i = digits.length-1; i>=0; i--){
                    carry = digits[i] + carry;
                    digits[i] = carry % 10;
                    carry = carry / 10;
                    if(carry == 0) return digits;
                }

                //carry will be 1 here, so initialise a new array 
                int[] nums = new int[digits.length+1];
                nums[0] = 1;
                return nums;
            }
        }
   

Since, this problem was easy and I was able to solve it quickly, I’m going to make it challenging by implementing a plusK algorithm. In this approach, instead of simply adding 1, k will be added to the input digits. I’ll be using this to solve the original plusOne problem. To implement this, I'll be using ArrayList instead of performing an in-place update.

Code Implementation

  
        public static int[] plusK(int[] digits, int k) {
            List result = new ArrayList<>();
            int carry = k;
            for(int i=digits.length-1;i>=0;i--){
                carry = digits[i] + carry;
                result.add(0,  carry%10);
                carry = carry/10;
            }

            while(carry>0){
                result.add(0,  carry%10);
                carry = carry/10;
            }
            return result.stream().mapToInt(Integer::intValue).toArray();
        }

        public int[] plusOne(int[] digits) {
            return plusK(digits, 1);
        }  
   

1. Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

2. Valid Parentheses

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
a. Open brackets must be closed by the same type of brackets.
b. Open brackets must be closed in the correct order.
c. Every close bracket has a corresponding open bracket of the same type.

1. Palindrome Partitioning

Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

2. Longest Palindromic Substring

Given a string s, return the longest palindromic substring in s.

1. Two Sum

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

2. Plus One

You are given a large integer represented as an integer array digits, where each digits[i] is the ith digit of the integer. The digits are ordered from most significant to least significant in left-to-right order. The large integer does not contain any leading 0's. Increment the large integer by one and return the resulting array of digits.

1. Three Sum

Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.

2. Container with most water

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]). Find two lines that together with the x-axis form a container, such that the container contains the most water. Return the maximum amount of water a container can store.

1. Search a 2D Matrix

You are given an m x n integer matrix matrix with the following two properties: Each row is sorted in non-decreasing order. The first integer of each row is greater than the last integer of the previous row. Given an integer target, return true if target is in matrix or false otherwise. You must write a solution in O(log(m * n)) time complexity.

2. Insert Interval

You are given an array of non-overlapping intervals intervals where intervals[i] = [starti, endi] represent the start and the end of the ith interval and intervals is sorted in ascending order by starti. You are also given an interval newInterval = [start, end] that represents the start and end of another interval. Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary). Return intervals after the insertion.

1. Reverse Linked List

Given the head of a singly linked list, reverse the list, and return the reversed list.

2. Merge Two Sorted Lists

You are given the heads of two sorted linked lists list1 and list2. Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists. Return the head of the merged linked list.

1. Swap Nodes in Pairs

Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)

2. Partition List

Given the head of a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x. You should preserve the original relative order of the nodes in each of the two partitions.