Algorithms Roadmap
Day 2: Valid Anagram
Problem Statement:
Valid Anagram - Given two strings `s` and `t`, return `true` if `t` is an anagram of `s`, and `false` otherwise.
Lets consider the following two approaches for this problem:
Approach 1: Sorting input strings
Anagrams return identical strings when sorted, so the simplest approach is to sort the input strings and compare. The input string can be sorted by splitting it into character array, performing the sort operation on the character array, and then join the sorted characters into a string.
Complexity: This approach uses extra O(n) space ( n = length of string) for character array and sorting the array makes it O(nlogn) time complexity.
Approach 2: Character frequency comparison
Second approach involves computing the frequency of each character in both strings. If any character’s frequency differs between the two strings, they are not anagrams. HashMap can be used to store the character frequencies since the updates can be done in constant time.
Complexity: This approach uses extra O(n) space for storing character HashMap. The time complexity is O(n) since we’ll be updating the HashMap for every character of the input strings.
Code Implementation:
Approach 1
class Solution {
private String sortedString(String s) {
char c[] = s.toCharArray();
Arrays.sort(c);
return Arrays.toString(c);
}
public boolean isAnagram(String s, String t) {
return sortedString(s).equals(sortedString(t));
}
}
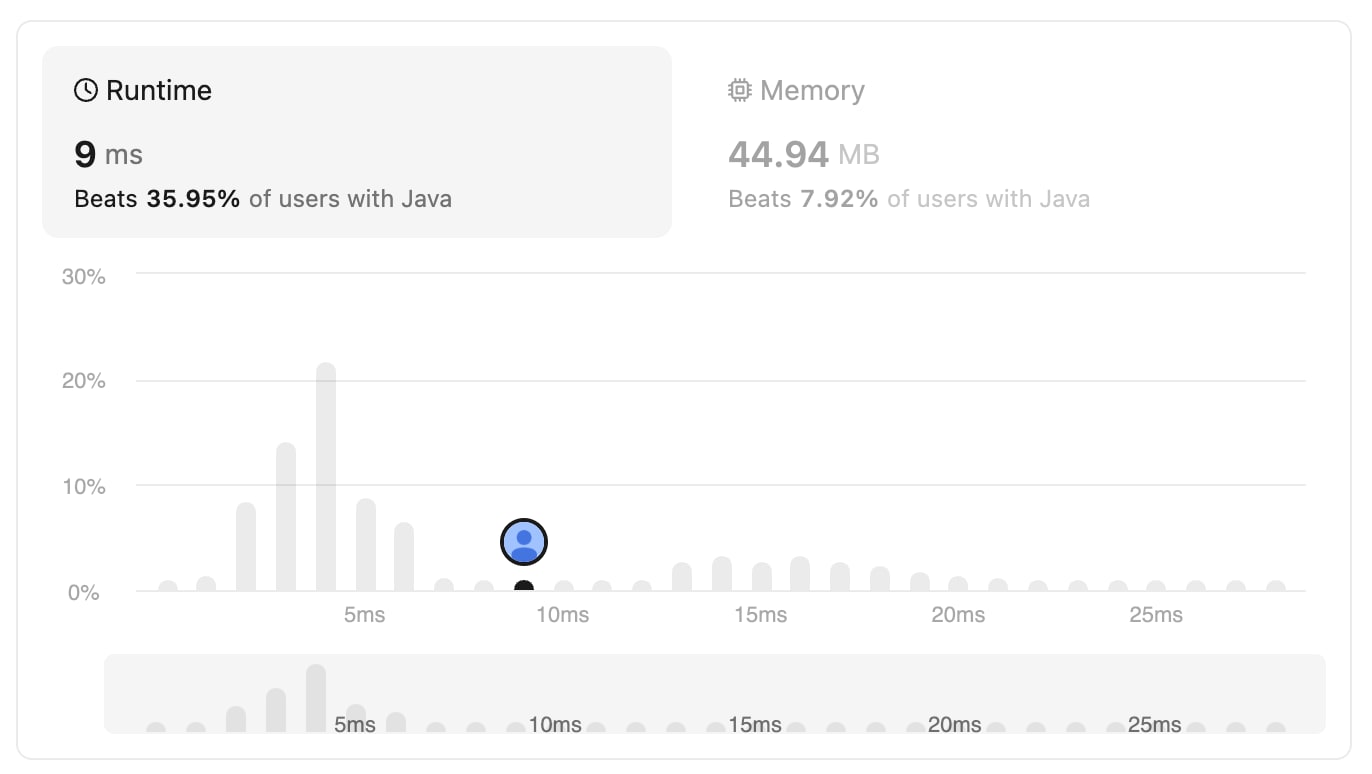
This implementation beats 35% users runtime which is acceptable. Arrays.toString(c) constructs the string via StringBuilder, it appends each character one by one, resulting in O(n) time complexity. Let’s explore if there would be any improvement by replacing it with String.valueOf(c) which takes constant time complexity.
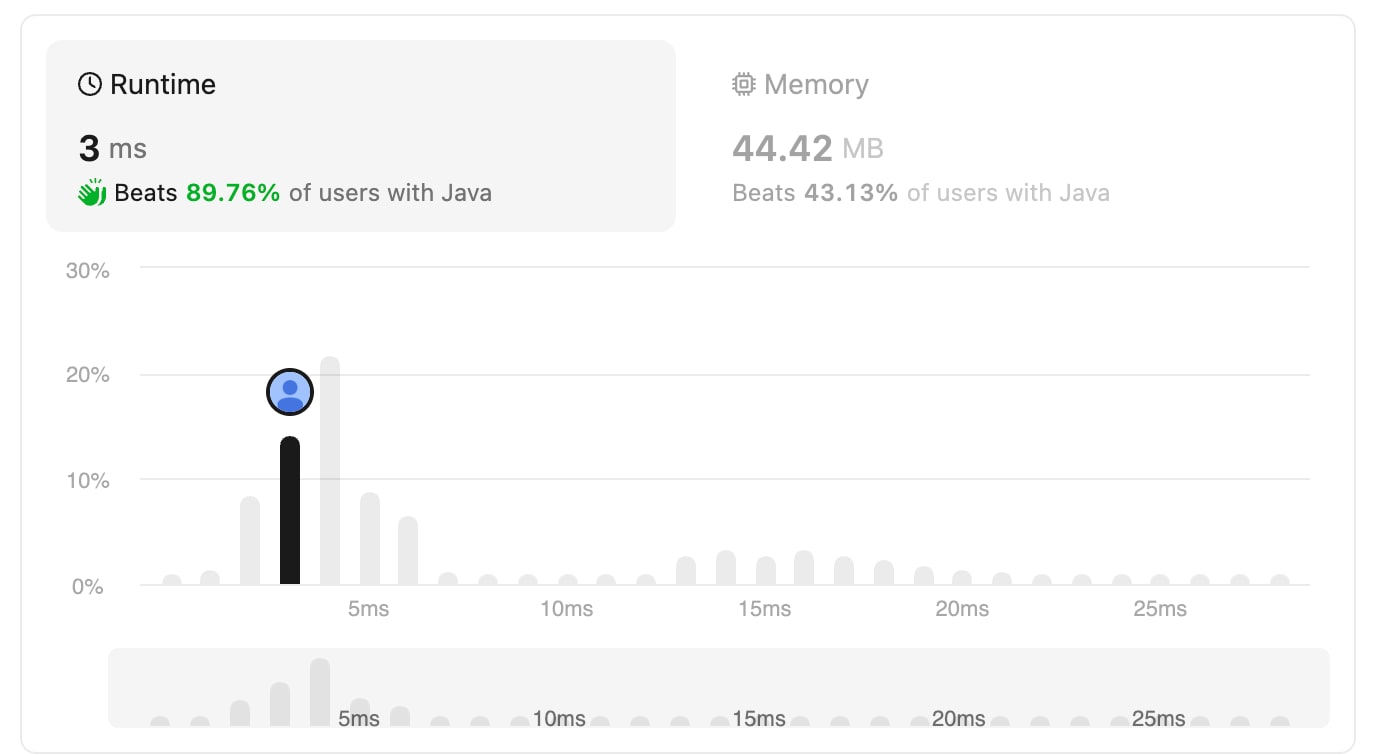
A single line change improved the runtime from 35% to 89%. Although, its only a minor improvement in memory but it beat 43% users compared to the previous 8%.
Approach 2
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
HashMap hm = new HashMap<>();
for (char c : s.toCharArray()) {
hm.put(c, hm.getOrDefault(c, 0) + 1);
}
for (char c : t.toCharArray()) {
if(!hm.containsKey(c) || hm.get(c)==0) return false;
hm.put(c, hm.get(c) - 1);
}
return true;
}
}
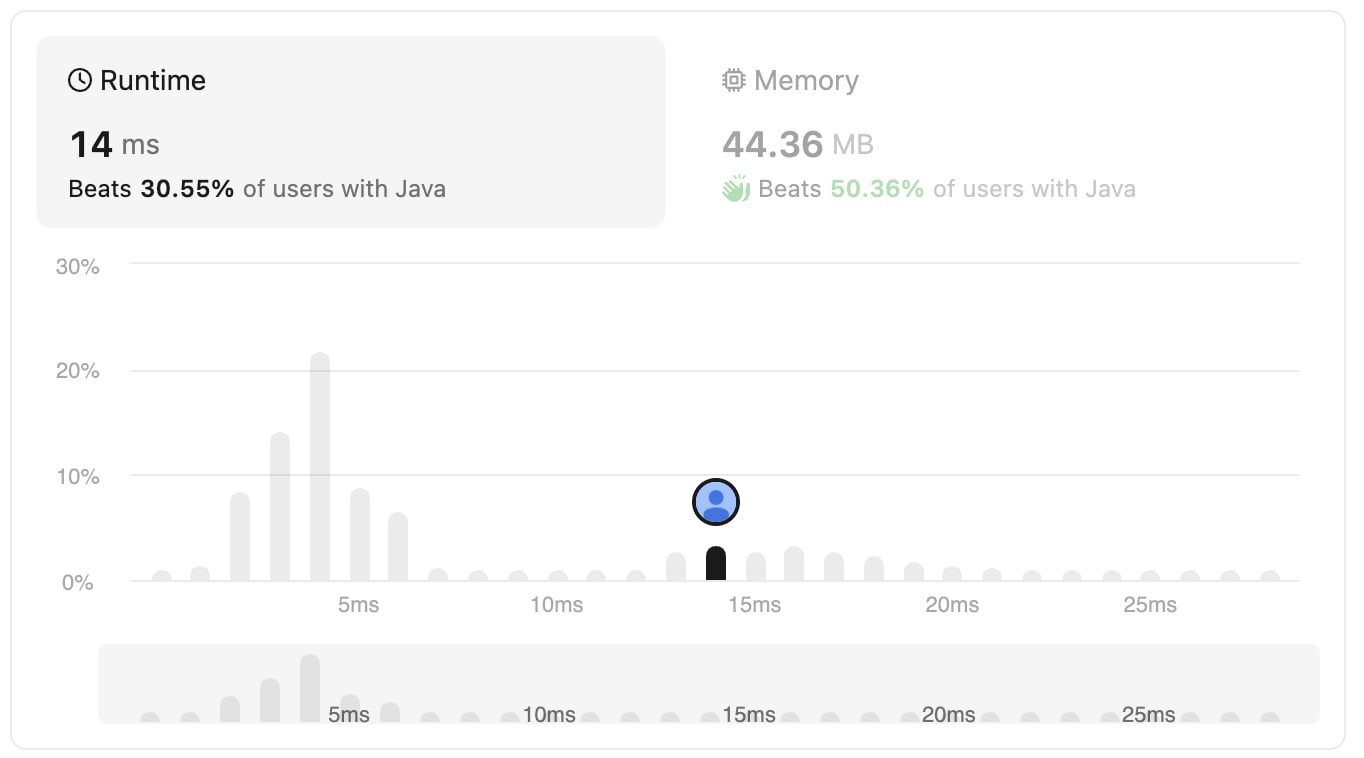
It's surprising to find that the approach 2 performed worse than approach 1. One possible explanation could be that there’s a constraint on the input string size, making log(n) effectively a constant. Going for a more complex approach by storing the frequencies of characters, didn’t provide any advantage.
Final thoughts
In an actual interview scenario, I would certainly choose the second approach, even if it appears to have lower performance in this specific case. Although this is a straight forward question, solving it sparked my curiosity.
We often prefer solutions with O(n) time complexity over those with O(nlogn), but does this translate to better performance in real-world scenarios?
Day 2 - Valid Anagram
Problem Statement:
Valid Anagram - Given two strings `s` and `t`, return `true` if `t` is an anagram of `s`, and `false` otherwise.
Lets consider the following two approaches for this problem:
Approach 1: Sorting input strings
Anagrams return identical strings when sorted, so the simplest approach is to sort the input strings and compare. The input string can be sorted by splitting it into character array, performing the sort operation on the character array, and then join the sorted characters into a string.
Complexity: This approach uses extra O(n) space ( n = length of string) for character array and sorting the array makes it O(nlogn) time complexity.
Approach 2: Character frequency comparison
Second approach involves computing the frequency of each character in both strings. If any character’s frequency differs between the two strings, they are not anagrams. HashMap can be used to store the character frequencies since the updates can be done in constant time.
Complexity: This approach uses extra O(n) space for storing character HashMap. The time complexity is O(n) since we’ll be updating the HashMap for every character of the input strings.
Code Implementation:
Approach 1
class Solution {
private String sortedString(String s) {
char c[] = s.toCharArray();
Arrays.sort(c);
return Arrays.toString(c);
}
public boolean isAnagram(String s, String t) {
return sortedString(s).equals(sortedString(t));
}
}

This implementation beats 35% users runtime which is acceptable. Arrays.toString(c) constructs the string via StringBuilder, it appends each character one by one, resulting in O(n) time complexity. Let’s explore if there would be any improvement by replacing it with String.valueOf(c) which takes constant time complexity.

A single line change improved the runtime from 35% to 89%. Although, its only a minor improvement in memory but it beat 43% users compared to the previous 8%.
Approach 2
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
HashMap hm = new HashMap<>();
for (char c : s.toCharArray()) {
hm.put(c, hm.getOrDefault(c, 0) + 1);
}
for (char c : t.toCharArray()) {
if(!hm.containsKey(c) || hm.get(c)==0) return false;
hm.put(c, hm.get(c) - 1);
}
return true;
}
}

It's surprising to find that the approach 2 performed worse than approach 1. One possible explanation could be that there’s a constraint on the input string size, making log(n) effectively a constant. Going for a more complex approach by storing the frequencies of characters, didn’t provide any advantage.
Final thoughts
In an actual interview scenario, I would certainly choose the second approach, even if it appears to have lower performance in this specific case. Although this is a straight forward question, solving it sparked my curiosity.
We often prefer solutions with O(n) time complexity over those with O(nlogn), but does this translate to better performance in real-world scenarios?
Sponsor Us|Community|Blog|Youtube|DLP
Have Feedback or want to contribute? Email: hello[@]100DaysOfCode.io
100DaysOfCode@2024